posted by Sam Toyer and Sylvie Thiébaux

Planning algorithms try to find series of actions which enable an intelligent agent to achieve some goal.

Such algorithms are used everywhere from manufacturing to robotics to power distribution.

In our recent paper at AAAI ‘18, we showed how to use deep learning techniques from vision and natural language processing to teach a planning system to solve entire classes of sophisticated problems by training on a few simple examples.

### Deep learning and planning

Deep learning is a popular technique for tasks like generating stylised captions for images, or learning how to play video or board games from images alone.

At a more abstract level, deep learning uses artificial neural networks with many layers (deep neural nets) to learn patterns in data.

For tasks where neural networks excel, there’s often a specific kind of network architecture which enables high performance.

For instance, recent image captioning work uses convolutional neural networks for visual processing and recurrent neural networks for text generation.

Despite its success in other areas, deep learning still has not seen wide application to automated planning.

We posit that this is due to a lack of network architectures for efficient, generalisable learning in a planning context.

There are many kinds of automated planning, but we focus on discrete probabilistic planning.

A probabilistic planner views each state of its environment as a truth assignment to a set of propositions (or binary variables).

In keeping with an AI tradition that stretches back to SHRDLU, we’ll start by considering how to control a simple block-stacking robot like that in Figure 1.

Such a robot might use several propositions:

• One proposition, (gripper-empty) to indicate whether the gripper is free to grasp another block ((gripper-empty) = True) or not ((gripper-empty) = False).
• A set of propositions of the form (on ?block1 ?block2) to indicate whether a pair of blocks, ?block1 and ?block2, are stacked on one another ((on ?block1 ?block2) = True) or not ((on ?block1 ?block2) = False).
• A set of propositions of the form (holding ?block) to indicate whether a specific block is sitting in the gripper ((holding ?block) = True), or not ((holding ?block) = False).
• …and so on.

The planner also has access to actions which can move the environment from state-to-state. In our running _blocks world_ example, it might have actions of the form "pick block A up from block B and hold it in the gripper". These actions may have stochastic outcomes (hence the probabilistic in probabilistic planning)—perhaps our robot might accidentally drop blocks from time to time when it tries to grasp them. The planner's goal is to suggest an appropriate action in each state which the agent visits such that following the planer's suggested actions will, with high probability and low cost, allow the agent to obtain some goal (e.g. to stack all blocks in a specific configuration). This general approach can be used to solve many problems ranging from classic puzzles (like Rubik's Cube or the aforementioned Blocks World) to real-world problems in robotics, transport, cyber-security, etc.

Probabilistic planning is hard partly because of the huge number of states which an agent might encounter.

A planning problem with $n$ variables could have up to $2^n$ states!

Current planners use domain-independent heuristics to guide their search towards goal states, thus allowing them to ignore all but a handful of environment states.

However, such planners are generally not able to learn from experience: if the heuristic over-estimates or under-estimates the “goodness” of a state, then it will continue to do so in future when it visits similar states.

The focus of our work is on using deep learning to teach planners how to choose appropriate actions in a planning problem, then generalise that knowledge to similar problems.

This greatly accelerates planning by allowing the planner to avoid making the same mistakes over and over again.

A neural network for planning

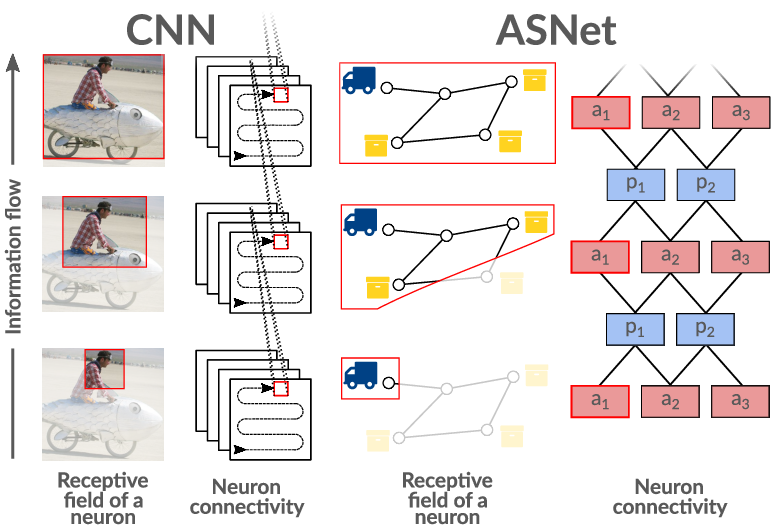
Our AAAI paper introduces a new form of deep neural networks, called ASNets, that are specifically designed to solve planning problems.

This new neural net architecture is designed to learn to solve any problem of a given planning domain, from the specification the “rules” of this domain, and examples of plans for small problems in this domain.

For instance, we can give ASNets a description of the blocks world puzzle, give it some example of plans for small blocks world problems, e.g. those with 4-7 blocks.

It will then learn to solve any blocks world problem, even with very large numbers of blocks.

Fig.2 (at right) gives a very high-level overview of the structure of our neural network, the ASNet.

Each planning problem corresponds to a (possibly distinct) ASNet which is automatically constructed using the structure of the problem.

The ASNet consists of alternating layers of action layers and proposition layers.

• Each action layer consists of an action module for each action in the corresponding problem; in intermediate layers, these action modules are like single-layer neural nets that take feature vectors from proposition modules as input and produce new feature vectors as output.

• Each proposition layer consists of a proposition module corresponding to each proposition in the original problem; again, each proposition module takes action module feature vectors as input and produces a single feature vector as output.

• The first layer is always an action layer in which action modules receive proposition truth values describing the current state, while the last layer is always an action layer in which action modules produce quantities representing the network’s confidence that each action is helpful.

• Within the same layer, weights are shared between action modules for similar actions and between proposition modules for similar propositions, which reduces the number of parameters that need to be learned.

We detail this full construction in our paper.

Importantly, the combination of weight sharing and specially-structured connectivity between modules ensures that two action schema networks corresponding to problems instantiated from the same domain will be able to share the same weights.

This holds even if the problems have a different number of actions and propositions (and thus a different action and proposition modules).

Hence, we can learn a set of weights by training the network on small problems from a domain, then transfer those learnt weights to solve large problems without having to re-train at all.

In other words, we can obtain a generalised policy: a mapping from states to appropriate actions which can be applied to any problem in a domain.

While there has been a great deal of past work on solving decision-making problems with neural networks—AlphaGo being one prominent example—most existing approaches are not able to generalise in the same way as ASNets.

For instance, AlphaGo would not be able to adapt from a 13x13 Go board (as used to train humans) to a (standard) 19x19 one without retraining.

The tasks that ASNets can currently solve are very different to Go, but the way that ASNets generalise planning knowledge with neural networks is, to the best of our knowledge, unique.

Further, we have found that the special structure of our network enables it to learn with very little data, in contrast to the famously data-hungry neural-net-based systems used in vision, reinforcement learning, and related areas.

### Quick planning and more

We can use ASNets for rapid planning on large planning problems.

We train the ASNet to choose good actions on a collection of small, related problems from the same domain as a single large one.

The training problems are small enough that we can quickly run a traditional heuristic search planner to figure out which actions are “good”, then use a normal classification loss to encourage the ASNet to choose similar actions to the heuristic search planner.

After the ASNet is trained, we can simply evaluate it on the large problem.

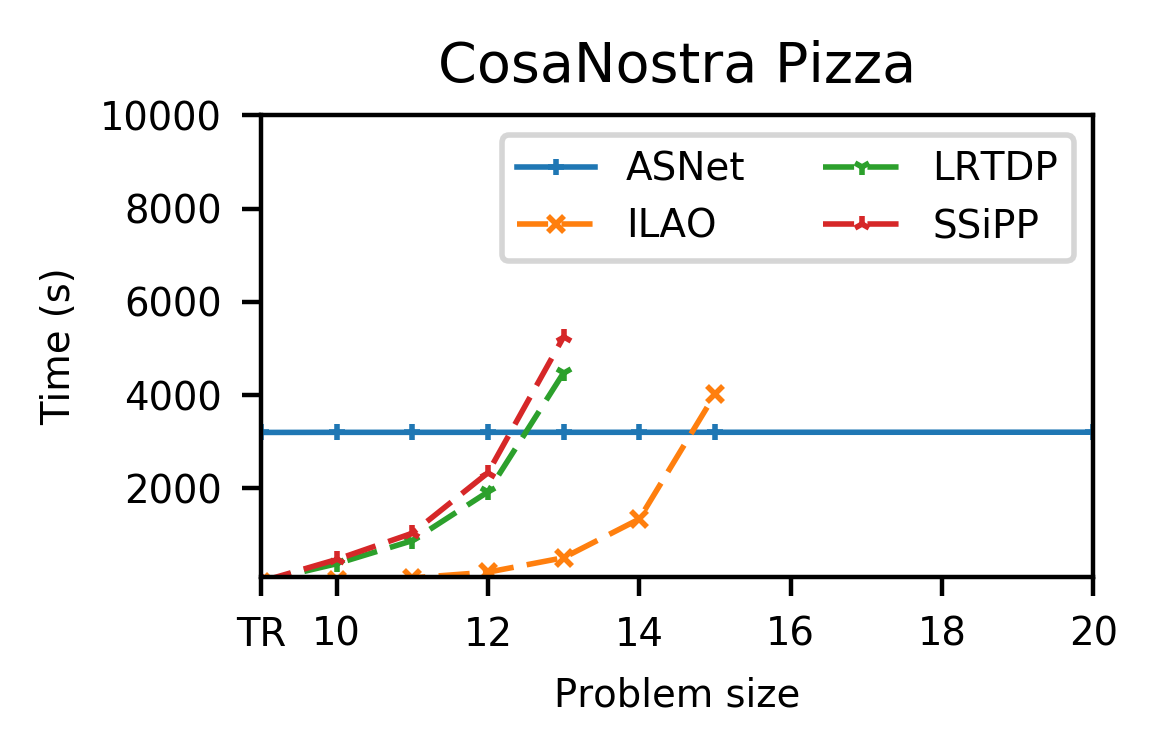
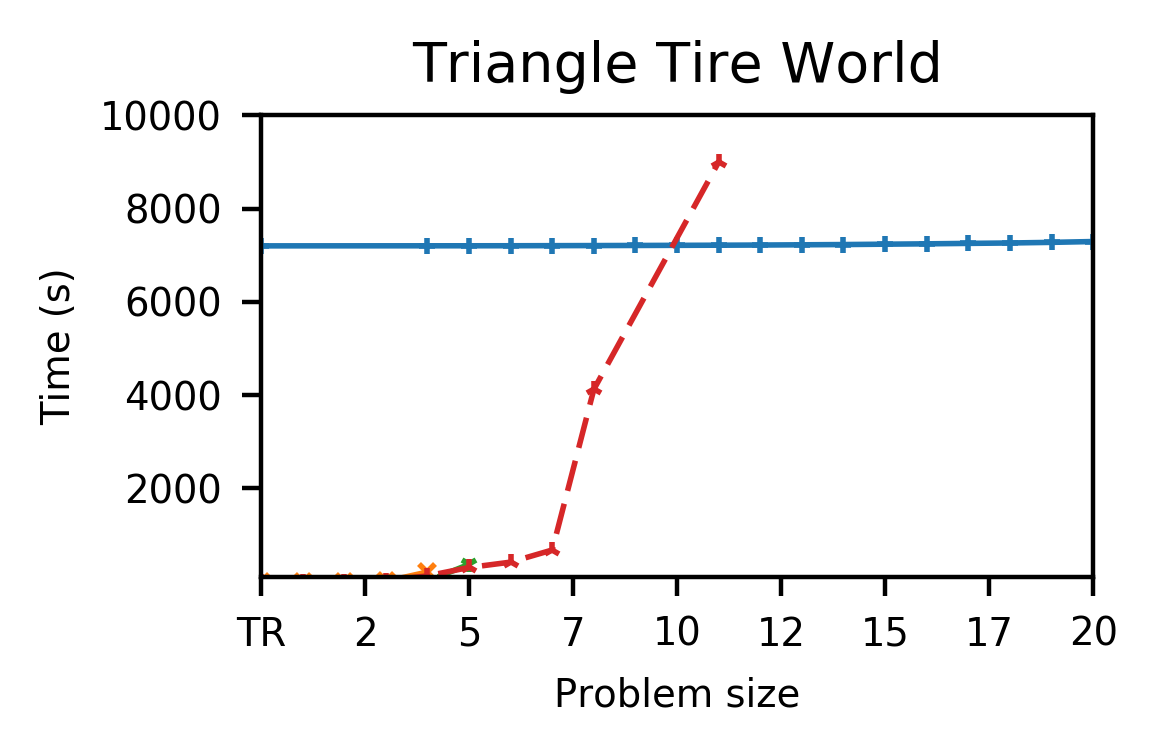
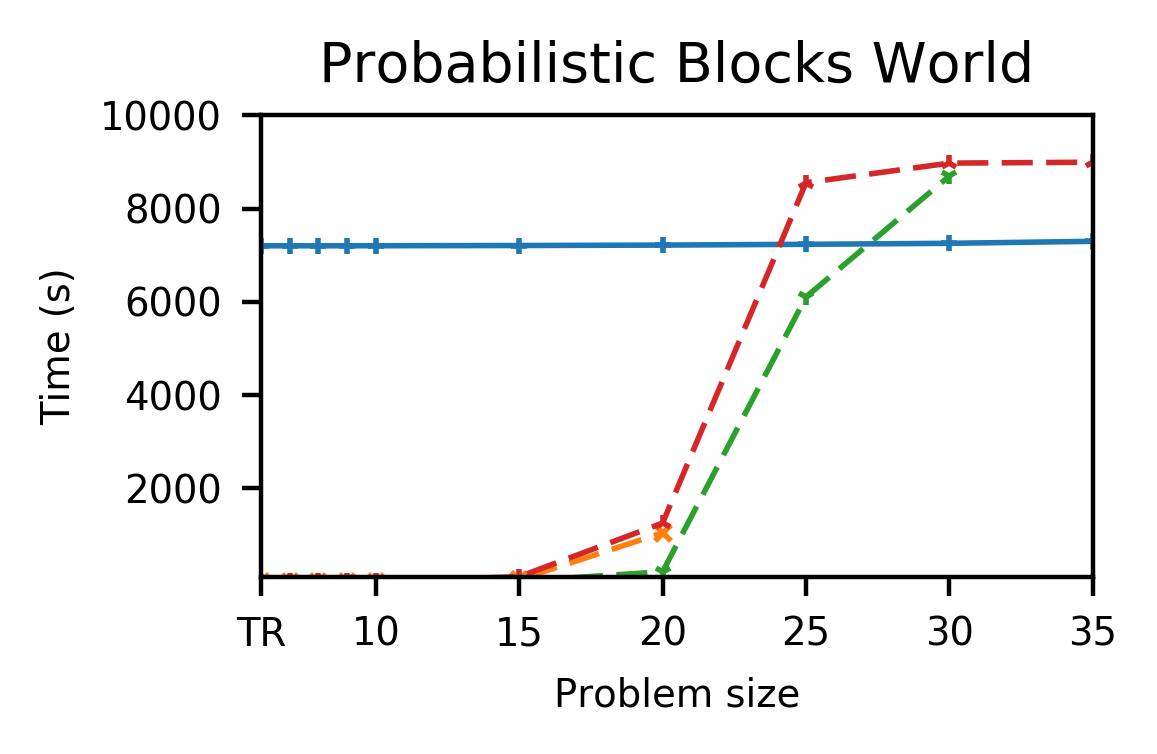
Fig.3 shows the outcome of this approach on three planning domains which are challenging for traditional planners.

After spending somewhere between a few minutes and a couple of hours training, our system is able to rapidly solve all tested problems in quick succession.

In contrast, the non-learning baseline planners struggle to solve the larger problems within our 2.5 hour cutoff.

Although we have only closely examined the use of ASNets for generalised policies, we believe that future generations of ASNets would connect deep learning methods to planning problems in more ways.

For instance, it may be possible to use ASNets to learn generalised heuristics and ranking functions.

We could also consider combining ASNets with traditional search; for example, by using an ASNet as the rollout policy in Monte Carlo Tree Search.

Finally, we note that ASNets are not closely tied to the particular planning formalism that we have considered; indeed, it could be possible to apply them to planning problems that have numeric state variables or partially observable states with little modification.

We leave all these promising avenues for future work.

To find out more about ASNets, check out our paper, code, AAAI oral slides, or the ANU News article “New intelligent system learns from simple problems to solve complex ones”.

Resources

Sam Toyer, Felipe Trevizan, Sylvie Thiebaux and Lexing Xie. Action Schema Networks: Generalised Policies with Deep Learning, in Proceedings AAAI Conference on Artificial Intelligence (AAAI ‘18), New Orleans, USA, 2018.

Download:	Paper PDF  |  Talk slides
Code & models:	Github repository
Bibtex:

@inproceedings{toyer2018action,
  title={Action Schema Networks: Generalised Policies with Deep Learning},
  author={Toyer, Sam and Trevizan, Felipe and Thi{\'e}baux, Sylvie and Xie, Lexing},
  booktitle={AAAI Conference on Artificial Intelligence (AAAI)},
  year={2018}
}